Наверх
НаверхПечально известная «диванная задача», которая десятилетиями ставила в тупик математиков, наконец-то может быть решена
Математическая задача об определении дивана самого большого размера, который можно пронести через угол, наконец-то решена, хотя это и не поможет вам при переезде.
На двадцать пять лет позже, чем нужно было Россу, чтобы занести свой новый диван в квартиру в сериале «Друзья», математик наконец-то решил назойливую «проблему дивана».
Математическая задача определяет диван самого большого размера, который может поместиться за углом заданной ширины — именно с этой проблемой столкнулись персонажи в эпизоде «Друзей», вышедшем в 1999 году. Просьбы Росса «Разворачивай!» можно было бы избежать, оказывается, если бы он только рассмотрел диван Гервера с 18 изогнутыми секциями и максимальной площадью 2,2195 единиц. (Ладно, может быть, это было бы не так уж и полезно.)
Решение проблемы дивана — это первое в математике. Проблема была поставлена австрийско-канадским математиком Лео Мозером в 1966 году. Мозер просил найти максимально возможную площадь одной фигуры на плоскости, которая могла бы пройти через прямой угол коридора с единичной шириной. Хотя это может показаться простым, математика довольно сложна, так как проблема включает в себя как максимизацию площади, так и движение формы.
Теперь Джинён Бэк, постдокторант-исследователь в области математики в Университете Йонсей в Южной Корее, нашел ответ. Бэк опубликовал свое решение 2 декабря на сайте препринтов ArXiv. На более чем 100 страницах математических доказательств Бэк обнаружил, что для коридора шириной в 1 единицу максимальная площадь воображаемого дивана может составлять 2,2195 единиц, что сужает ответ с ранее известного диапазона от 2,2195 до 2,37 единиц. Доказательство еще не было опубликовано в рецензируемом журнале и должно быть проверено другими математиками, чтобы определить, является ли оно действительно оптимальным.
«Гервер» в названии дивана Гервера — это математик Джозеф Гервер, почетный профессор Ратгерского университета, который в 1992 году предположил нижнюю границу в 2,2195. Но велись споры о том, может ли диван быть больше, и в 2018 году команда, используя компьютерное доказательство, предположила, что 2,37 на самом деле является верхней границей.
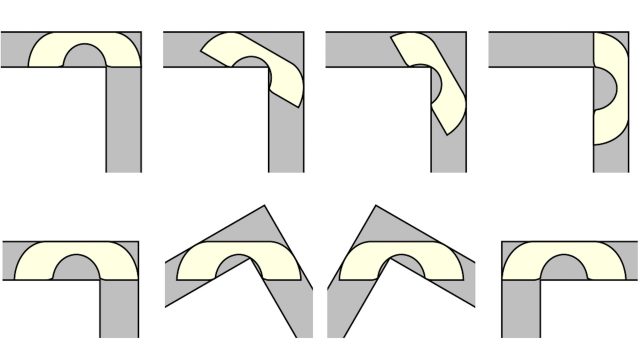
Диван Гервера — это широкий U-образный диван с изогнутым «сиденьем», который может протиснуться за угол, не застревая. Вопрос заключался в том, действительно ли этот кропотливо разработанный диван, состоящий из 18 отдельных кривых, был самой большой, самой оптимальной формой, которая могла бы совершить поворот. Бэк проработал геометрию формы и ее движение и обнаружил, что решение Гервера, по сути, было правильным.