 Наверх
Наверх9 самых огромных чисел, известных человечеству
От скромного триллиона до числа Грэма — подборка самых огромных чисел, когда-либо придуманных человеком.
Большие числа встречаются повсюду: от клеток человеческого тела до размеров Вселенной. Но как только числа выходят за рамки физического, человеческому разуму становится трудно постичь их невероятный масштаб. Даже бесконечность может показаться более понятной — она просто продолжается и продолжается. А когда числа становятся достаточно большими, всё начинает сливаться воедино, как сказал в 2013 году в интервью Live Science покойный Джон Борвейн, специалист по прикладной математике из Университета Ньюкасла в Австралии.
«Мы не понимаем, что означают цифры такого масштаба», — сказал Борвейн.
От скромного триллиона до числа Грэма — вот некоторые из самых невероятных чисел.
Большое — это относительно

Если говорить о личном бюджете, то $31,4 триллиона долларов в качестве потолка госдолга кажутся чем-то невообразимым. Но в масштабах атомов во Вселенной эта сумма выглядит ничтожно малой, как сказал в 2013 году Live Science Скотт Ааронсон, учёный-компьютерщик, ранее работавший в Массачусетском технологическом институте, а теперь в Техасском университете в Остине.
Чтобы попытаться понять огромные числа, большинство людей прибегают к масштабным аналогиям. Например, Карл Саган сравнил возраст Вселенной с календарным годом, а людей — с теми, кто появляется в последние несколько часов перед Новым годом.
Гипотеза Римана
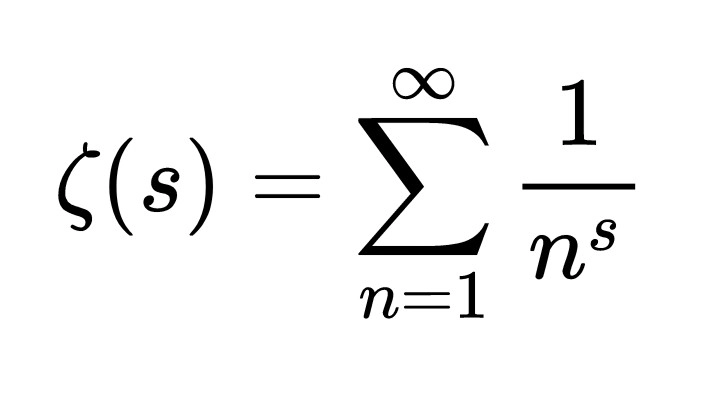
Гипотеза Римана, впервые сформулированная в 1859 году, является одной из величайших нерешённых математических задач, и тот, кто её решит, получит премию в размере 1 миллиона долларов. Гипотеза заключается в том, что действительная часть каждого нетривиального нуля определённой функции, метко названной дзета-функцией Римана, равна 1/2.
«Это самый большой нерешённый вопрос в математике, который гарантирует, что ваше имя будет известно через 10 000 лет», — сказал Борвейн.
Если гипотеза верна, она имеет важное значение для распределения простых чисел, которые делятся только на себя и на единицу. Чтобы проверить гипотезу, математики ищут чрезвычайно большие простые числа — те, что больше 10 в 30-й степени, сказал он. Это может показаться абстрактным, но у этого есть множество практических применений, сказал Борвейн. «Простые числа используются во всём, что мы применяем для шифрования», — сказал он. «Всё это зависит от того, что алгоритмы разрабатываются с использованием свойств простых чисел, которые, как мы думаем, верны, но мы этого не знаем».
Вселенная

Ещё во времена Архимеда философы задавались вопросом, сколько мельчайших частиц может поместиться в Вселенной. Архимед подсчитал, что Вселенная может быть заполнена примерно 10 в 63-й степени песчинками. Он использовал ряд крайне приблизительных оценок: количество маковых зёрен в одной песчинке, количество песчинок, которые покрывают длину стадиона, и расстояние между Землёй и Солнцем в стадиях, сказал Генри Менделл, историк античности из Калифорнийского государственного университета в Лос-Анджелесе.
Несмотря на приблизительность его расчётов, он был недалёк от истины. По современным оценкам, общее количество атомов во Вселенной составляет около 10 в 82-й степени.
Фактор космологической неопределённости

Когда Эйнштейн вывел свои уравнения теории относительности, он включил в них небольшую константу, называемую космологической постоянной, чтобы учесть тот факт, что Вселенная стационарна. Хотя позже он отказался от этой константы, когда узнал, что Вселенная расширяется, оказалось, что гений был на верном пути: учёные считают, что космологическая постоянная, равная всего лишь 10 в минус 122-й степени, даёт представление о тёмной энергии, которая загадочным образом ускоряет расширение Вселенной, рассказал Ааронсон Live Science в 2013 году.
Космологическая постоянная была огромной головной болью для учёных, потому что предсказания отличались от измерений константы на 120 порядков. На протяжении многих лет физики пытались объяснить это несоответствие, изменяя другие параметры, например, то, как меняется масса частиц с течением времени, как ранее сообщала Live Science.
Геракл и Гидра

Иногда нужно, чтобы что-то стало большим, прежде чем оно станет маленьким. В 1982 году математики Джефф Пэрис и Лори Кирби задали загадку: представьте, что Геракл сражается с гидрой, у которой вместо голов — деревья. Если он отрубит одну голову, у мифического чудовища просто вырастет определённое количество новых голов в соответствии с несколькими правилами. Удивительно, но Геракл в конце концов всегда побеждает гидру и отрубает ей все головы.
Но даже если Геракл будет умным и выберет наиболее эффективную стратегию, у Гидры сначала вырастет больше гуголплексов голов (или 10 в степени 10 в степени 100).
Простые числа Мерсенна

Простые числа Мерсенна — это класс чисел, которые быстро становятся большими. Эти простые числа равны 2 в степени простого числа минус 1. Первые несколько чисел невелики — 3, 7, 31, — но они очень быстро становятся невероятно большими. Примерно до 1951 года было известно только 12 таких простых чисел, но к этому году (2024) их стало 52.
Чтобы справиться с этими гигантскими числами, учёные используют проект Great Internet Mersenne Primes Search (GIMPS), который задействует вычислительные мощности тысяч интернет-пользователей для поиска неуловимых простых чисел.Самое большое известное простое число было обнаружено в октябре 2024 года исследователем-любителем и бывшим сотрудником Nvidia Люком Дюрантом. Число 2136 279 841 – 1 состоит из колоссальных 41 024 320 цифр, что более чем на 16 миллионов цифр больше, чем у предыдущего рекордсмена, который также был открыт GIMPS шестью годами ранее.
Триллион треугольников
Около 1000 лет назад персидский математик Аль-Караджи впервые задался вопросом о том, сколько существует конгруэнтных чисел. Но что такое конгруэнтные числа? Это числа, равные площади прямоугольных треугольников со сторонами, равными целым числам или дробям. Таким образом, площадь треугольника со сторонами 3, 4 и 5 будет равна ½ * 3 * 4 = 6, то есть 6 — это конгруэнтное число.
Потребовалось ещё одно тысячелетие, прежде чем были открыты первые сто конгруэнтных чисел. Однако к 2009 году суперкомпьютеры открыли первые 3 148 379 694 конгруэнтных числа. Некоторые из этих чисел настолько велики, что если записать их цифры в десятичной системе, то они дотянутся до Луны и обратно. По словам Борвейна, гигантские числа имеют интересное применение в хранении данных, поскольку они настолько велики, что случайный гамма-луч может нарушить битовую структуру этих чисел и сделать их неверными.
Число Грэма

Все эти числа меркнут по сравнению с числом Грэма — настолько большим числом, что попытка запомнить все его цифры превратит вашу голову в чёрную дыру. Это число, которое в какой-то момент стало самым большим числом, когда-либо использовавшимся в математическом доказательстве, возникло в ответ на простую загадку о том, как распределить людей по определённому набору комитетов с учётом нескольких ограничений.
Хотя математики уверены, что для решения задачи нужно как минимум 13 человек, в 1970-х годах математик и жонглёр Рональд Грэм пришёл к выводу, что количество людей должно быть меньше числа Грэма. Чтобы просто вычислить это число, нужно сделать 64 шага и перемножить безумно огромное количество троек.
Это число невозможно записать в экспоненциальном представлении, вместо этого его нужно записать с помощью ряда стрелок вверх, обозначающих ряды степеней. Позже Грэм показал, что верхняя граница для этой загадки намного меньше числа Грэма, но всё равно огромна.
Число TREE(3)
Хотя число Грэма было одним из самых больших чисел, предложенных для конкретного математического доказательства, с тех пор математики пошли ещё дальше. В 1998 году логик Харви Фридман из Университета штата Огайо предложил головоломку, в которой нужно было определить, какой длины должна быть последовательность букв, чтобы в ней были заданы определённые параметры повторяющихся отрезков букв. Хотя ответ не бесконечен, он очень велик.
Полученное Фридманом число TREE(3) вычисляется путем создания все более массивных башен из двоек, возведенных в степень двойки, с помощью так называемых функций Аккермана. Чтобы было понятнее, четвертая функция Аккермана предполагает возведение двойки в степень 65 536 двоек. Но TREE(3) намного, намного больше этого числа — настолько больше, что по сравнению с ним число Грэма кажется крошечной пылинкой.
«Эти более высокие уровни масштабности размыты, и невозможно отличить один уровень масштабности от другого», — написал Фридман в своей статье.
Примечание редактора: эта статья была опубликована в 2013 году и обновлена 17 ноября 2023 года с учётом новой информации о наибольшем простом числе, атомах в наблюдаемой Вселенной и космологической постоянной. Статья была обновлена в октябре 2024 года после открытия нового наибольшего простого числа.
Математический прорыв: найден революционный способ выявлять простые числа!







